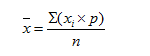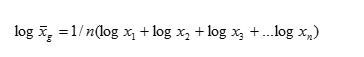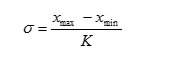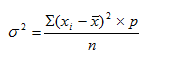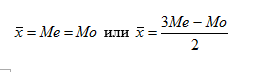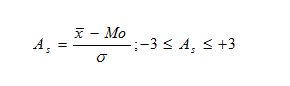Вариационные ряды — помощь в оценке распределения явлений по величине признаков

Вариационный ряд (frequency table)- ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через «х». Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через «р».

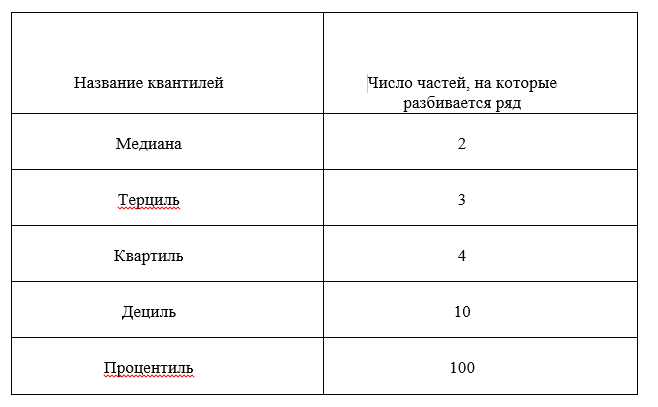
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице:

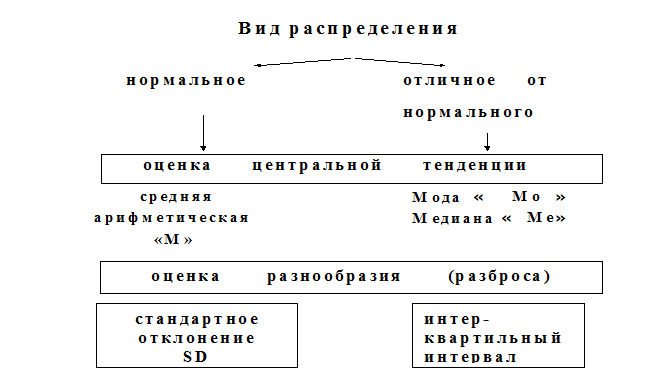
Рис. 1 Этапы описания (обобщения) количественного признака

Виды вариационных рядов

Вариационные ряды могут быть следующих видов:

1. В зависимости от вида случайной величины :

— дискретный;

— непрерывный .

2. В зависимости от группировки вариант:

— несгруппированный;

— сгруппированный (интервальный):

3. В зависимости от частоты, с которой каждая варианта встречается в вариационном ряду:
   • простой ( р =1);
   • взвешенный ( р >1).

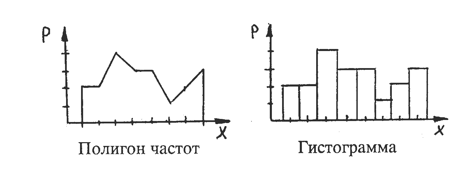
Графическое изображение вариационных рядов

где  х — варианты, р — частоты.

Основные характеристики вариационного ряда

Такие характеристики зависят от оцениваемых показателей:

1). Показатели, характеризующие центральную тенденцию (central tendency) или уровень ряда: средние величины или меры расположения (собственно средние и структурные средние).

2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс) (spread) признака: стандартное отклонение, дисперсия, размах, интерквартильный интервал.

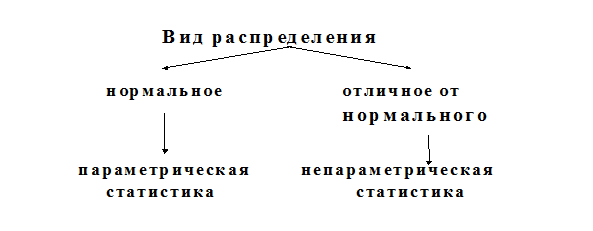
Выбор характеристик центральной тенденции и разнообразия признака прежде всего зависит от вида распределения. В случае нормального распределения используют показатели параметрической статистики, в случае распределения, отличного от нормального и при неизвестном виде распределения применяют показатели непараметрической статистики.

Средние величины

Средняя величина — обобщающий коэффициент, который характеризует наиболее типичный размер определенного признака в целом для совокупно­сти или для отдельных ее частей. Расчет средних величин имеет смысл только для качественно однородной совокупности, в связи с этим в одной совокупности может быть столько средних, на сколько однородных групп она может быть разбита.

Виды средних величин

Средняя арифметическая(mean) — применяется, если варианты возрастают (убывают) в арифметической прогрессии.

х — средняя арифметическая;

x_i — варианта;

р — частота встречаемости варианты;

n — число наблюдений

Свойства средней арифметической:

— носит обобщающий характер;

— имеет абстрактное значение;

— алгебраическая сумма отклонений отдельных вариант от средней равна 0 (сущность средней и способ проверки правильности расчета средней);

— сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, неравной средней;

— сумма произведений отдельных вариант на свои частоты равна произведению средней на число наблюдений (единство суммарного действия и способ провер­ки правильности расчета средней);

— если каждую из вариант увеличить или уменьшить на определенное число (в определенное число раз) ,то средняя арифметическая увеличится или уменьшится на столько же (во столько же);

— если частоту всех вариант пропорционально изменить, то средняя арифметическая от этого не изменится.

Средняя геометрическая — вычисляется, если варианты возрастают (убыва­ют) в геометрической прогрессии.

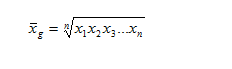На практике используют логарифмированную формулу:

Структурные средние

Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном ряду   варианта.

Мода используется:

• при малом числе наблюдений, когда велико влияние состава совокупности
  на среднюю ;
• для характеристики центральной тенденции при ассиметричных распределениях, когда велико влияние на среднюю крайних вариант;

Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные

части. Медиана используется:

• при необходимости знать, какая часть вариант лежит выше и ниже

средин­ного значения ;

• для характеристики центральной тенденции при ассиметричных распределениях

Характеристики разнообразия вариационного ряда

1. Размах вариации (амплитуда) (range): А = Х_mах — X_min
2. Стандартное отклонение (среднее квадратическое отклонение) (standard deviation, SD)

— приблизительный расчет стандартного отклонения по амплитуде:

где К — коэффициент Ермолаева, рассчитывается по специальной таблице с учетом числа наблюдений (см. приложение).

При числе наблюдений больше 30:

Стандартное отклонение наиболее часто используется при определении нормы и патологии, в основе которого лежит «правило трех сигм», справедливое только для нормального распределения.

Сводная таблица формул

для нахождения средних значений и мер рассеяния

Примечание: не стоит путать пары обозначений и , а также   и s (SD) между собой. Они обозначают схожие вещи, но в разных совокупностях (мю и сигма относятся к генеральной совокупности, выборочная средняя и стандартное отклонение к выборочной средней). Подробнее в главе «Выборочный метод».

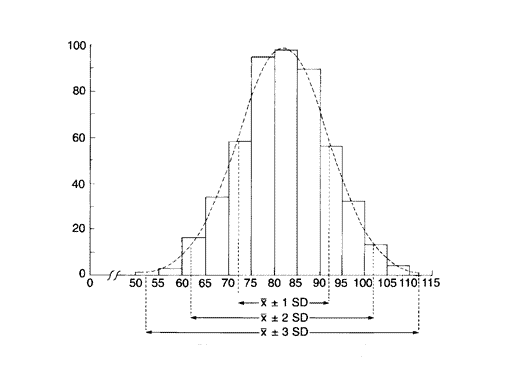
 «Правило трех сигм»

68.3 % всех вариант отклоняются от своей средней не более, чем на s

95.4% вариант находятся в пределах X ± 2s

99.7% вариант находятся в пределах X ± 3s

Отклонение параметра от его средней арифметической в пределах  s расценивается как норма, субнормальным считается отклонение в пределах  ± 2s и патологическим — сверх этого предела, т.е. > ± 2s» (рис. )

Рис.3  Правило «трех сигм» ( SD – стандартное отклонение).

3. Дисперсия (варианса) (variance)

При распределении Пуассона дисперсия равна средней:  

4. Коэффициент вариации (variation coefficient):

Вариационный ряд считается однородным при C_v <10 % , обладающим средней вариабельностью (разнообразием) при С_v =10-15% и обладающим значительной вариабельностью при C_v >15% .

Коэффициент вариации используется при сравнении вариационных рядов, имеющих различную размерность, или одной размерности, но обладающими резкими различиями в своих значениях, затрудняющими их сопоставление.

5. Интерквартильный интервал (inter-quartile range, IQR)

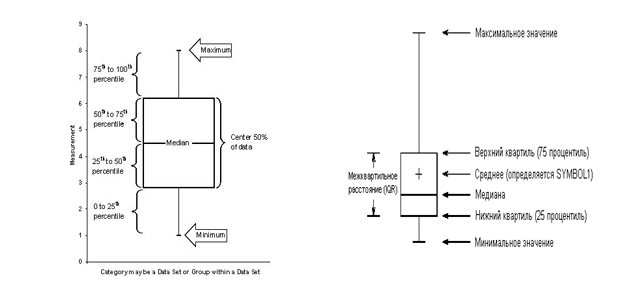
Вариационный ряд разбивают на четыре интервала, получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним (low quartile) и верхним квартилями(high quartile). 50% квантиль – это медиана. Внутри интерквартильного интервала  (между 25% и 75% квантилями) лежат 50% наиболее типичных (близких к центральному) значений.

Таким образом, в случае нормального распределения вариационный ряд описывается средней величиной и стандартным отклонением, если распределение неизвестно или оно отлично от нормального, центральную тенденцию и разброс можно описать с помощью медианы, нижнего и верхнего квартиля (интерквартильным интервалом).

Рис.4   Графическое представление описательной статистики (коробчатый график, «коробка с усами», box-plot)

Проверка нормальности распределения

Соответствие экспериментального распределения нормальному проверяется следующими способами:

1. По числам Вестергарда при нормальном распределении в пределах:

х ± 0.3 s находится 25 % всех единиц наблюдения;

х ± 0.7 s находится 50 % всех единиц наблюдения;

х ± l,l s находится 75 % всех единиц наблюдения;

х ± 3,0 s находится 99 % всех единиц наблюдения.

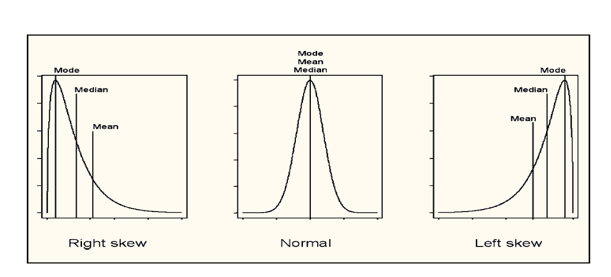
2. По соотношению средней арифметической и структурных средних:

— при нормальном распределении, которое обладает симметричностью:

или

— правило «двух третей» Юла:

а). если распределение симметрично: Me = Mo;

б). если распределение обладает правосторонней асимметрией: Me > Mo;

в). если распределение имеет левостороннюю асимметрией Me < Mo

3. По коэффициенту асимметрии (skewness):

а) если распределение симметрично: A _s = 0

б) при правосторонней асимметрии:  A _s > 0

в) при левосторонней асимметрии: A _s < 0

Рис. 5  Графическое изображение симметричного и асимметричного распределений

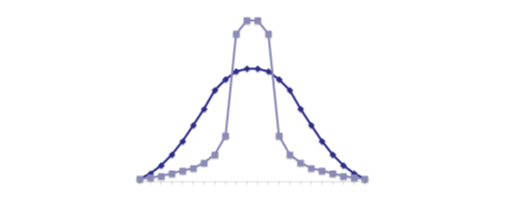
4. По показателю эксцесса или показателю островершинности (kurtosis) мера остроты пика распределения случайной величины. Показатель эксцесса нормального распределения составляет 3. Стоит запомнить, что помимо возможной асимметрии вариационного ряда, также стоит оценивать высоту колоколообразной кривой, так как не все симметричные вокруг средней гистограммы вариационного ряда можно считать нормально распределенными.

Вершина более крутая, чем для нормального распределения: эксцесс положительный, имеются длинные хвосты распределения;
Вершина более пологая, чем у нормального распределения: эксцесс отрицательный, имеются короткие хвосты распределения.

5. Если Ме занимает срединное положение между 25-м и 75-м процентилем, то распределение близко к нормальному.

Так как значительная часть статистических методов (параметрическая статистика) основана на предположении, что распределение близко к нормальному, то, если экспериментальные данные не ложатся на кривую нормального распределения, их пытаются преобразовать таким образом, чтобы полученная кривая соответствовала нормальному распределению. Наиболее часто используются следующие способы «нормализующего преобразования» (transformation to normality) данных:

• гармоническое преобразование: 1 /х;
• извлечение квадратного корня: 
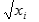
• логарифмирование {дает наиболее точное приближение}: log x_i
  Успешность преобразования данных оценивают по коэффициенту асимметрии: чем ближе он к 0, тем ближе экспериментальное распределение к нормальному.

6. Тесты на нормальность:

• Шапиро-Вилка (Shapiro-Wilk)
• Колмогорова-Смирнова (Kolmogorov-Smirnov)
• Крамера-вон Майса (Kramer-von Mises)
• Андерсона-Дарлинга (Anderson-Darling)

Исключение «выскакивающих» вариант

Иногда в небольших совокупностях встречаются варианты резко отличающи­еся по своему значению от других, так называемая «выскакивающая» варианта (outlying case). Если данное отличие обусловлено случайными колебаниями изучаемой величины, то такие варианты оставляют в совокупности и включают в общее число наблюдений. Если отличие обусловлено ошибками в исследовании или его причину точно нельзя установить, то «выскакивающие» вари­анты необходимо исключить из исследования.

Методика исключения вариант:

1)рассчитываются средняя величина и стандартное отклонение без учета «выскакивающих» вариант;

2)анализируется соотношение:

— если Х_выск — х, > s × f, то «выскакивающая» варианта исключается из  исследования;

• если х_выск — х < s × f то «выскакивающая» варианта должна быть включена в исследование.

При этом f – коэффициент Романовского, который определяется по специальной таблице с учетом числа наблюдений и вероятностью исключения варианты.

Whirlpool4396841 Filters uses state of the art technology to help remove Chlorine, Lead, Mercury, Cadmium, and Thallium.
SAME GREAT QUALITY AT A FRACTION OF THE PRICE — Experience the same quality of filtration without any sacrifice to the water flow rate. Whirlpool 4396841 Water Filter is also nearly half the cost as the manufacturer’s primary filter.
CHANGE YOUR FILTER EVERY 6 MONTHS — For optimum performance it’s recommended you change your filter every 6 months. Included with your purchase is a set of reminder stickers to help alert you when it’s time to change.

Мы уверенны, что с помощью нашей статьи читатели почерпнули для себя всю необходимую информацию о таком понятии, как вариационные ряды, средние величины. Наши авторы постарались максимально широко осветить необходимость данных видов исследования, их последовательность и результаты, которые при освоении методикой можно получить.

Благодарим за интерес, проявленный к нашей статье. Оставайтесь с нами!