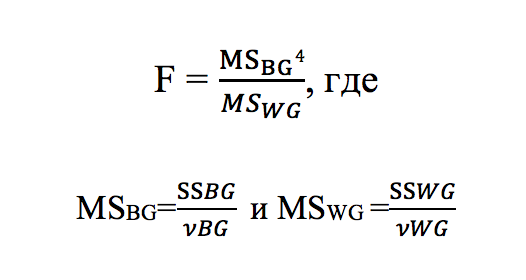Дисперсионный анализ ANalysis Of VAriance (ANOVA) просто о сложном

Кирилл Сергеевич Мильчаков
В данной статье пойдет речь о сути применения дисперсионного анализа и смысле это процесса. Казалось бы зачем мне нужен дисперсионный анализ (ANOVA) если существует такой прекрасный и понятный статистический критерий, как т-критерий Стьюедента? Однако, здесь стоит внимательно разобраться. Главное ограничение т-критерия перед дисперсионным анализом состоит в том, что первый предназначен для парных сравнений, то есть ситуации, когда у нас есть только две группы и он нуждается в поправках на множественные сравнения, в случае, если у нас более двух групп, во-вторых представим, если у нас 6 групп и мы ищем статистически значимые различия между ними, сколько попарных сравнений в таком случае нужно сделать? Много 🙂
В таком случае гораздо проще использоваться критерий, который предназначен для ситуаций, когда много групп и который нам даст единый ответ на все изучаемые группы — дисперсионный анализ.
Видео-версия статьи
Условия применения дисперсионного анализа ANOVA
Перед тем как приступить к применению дисперсионного анализа, который предназначен для минимизации риска неправильной оценки ошибки 1 рода в случае множественных сравнений необходимо убедиться в соблюдении ряда условий:
- Количественный непрерывный тип данных, дискретные данные менее желательны.
- Независимые между собой выборки.
- Нормальное распределение признака в статистических совокупностях, из которых извлечены выборки.
- Равенство (гомогенность) дисперсий изучаемого признака в статистических совокупностях из которых извлечены выборки, проверяется с помощью критерия Levene.
- Независимые наблюдения в каждой из выборок.
Статистическая информация для применения однофакторного дисперсионного анализа
Ho в случае однофакторного дисперсионного анализа (ANOVA) подразумевает, что средние генеральных совокупностей из которых были извлечены выборки равны, другими словами все они относятся к одной генеральной совокупности и различия носят случайный характер. Для проверки теорий в случае дисперсионного анализа используется F-распределение. F-статистика принимает только положительные или нулевые значения.
Процедура дисперсионного анализа состоит в определении соотношения систематической (межгрупповой) дисперсии к случайной (внутригрупповой) дисперсии в измеряемых данных. В качестве показателя изменчивости используется сумма квадратов отклонения значений параметра от среднего: SS (от англ. Sum of Squares). Общая сумма квадратов SSTotal раскладывается на межгрупповую сумму квадратов SSBG[1] и внутригрупповую сумму квадратов SSWG[2]:
SSTotal = SSBG + SSWG
В случае если верна Ho, то как внутригрупповая, так и межгрупповая дисперсии служат оценками одной и той же дисперсии и должны быть приблизительно равны.
Исходя из этого значение F должно быть близко к 1 в случае, если статистически значимых различий все-таки нет. Критическое значение F определяется уровнем значимости (обычно 0,05 или 0,01) и внутригрупповым и межгрупповым числом степеней свободы (ν). Оно достаточно сложно для вычисления, поэтому чаще используются табличные значения с указанием α, νBG, νWG.
Межгрупповое число степеней свободы:
νBG = m – 1.
m – число групп
Внутригрупповое число степеней свободы:
νWG = n – m
n – количество наблюдений в каждой из групп
Апостериорные значения
Однако, при обнаружении статистически значимых отличий мы не сможем сказать лишь об их наличии, но какие именно группы отличаются друг от друга мы определить не сможем, для этого производят так называемые процедуры апостериорных сравнений. Апостериорные сравнения представляют собой попарные сравнения изучаемых групп для обнаружения различий между ними.
Апостериорные сравнения могут быть проведены с помощью критерия Стьюдента для независимых выборок, что может показаться странным, учитывая сказанное ранее о проблеме множественных сравнений. Однако в отличие от простых попарных сравнений при проведении апостериорных сравнений рассчитываются новые критические уровни значимости для удержания ошибки 1 типа в пределах 5 %.
Наиболее простым и наиболее популярным способом коррекции ошибки 1 типа является поправка Бонферрони (Bonferroni), при которой уровень ошибки 1 типа делится на количество сравнений для получения нового критического уровня значимости. Так, если имеется 3 сравнения, то новый критический уровень должен быть 0,05 / 3 = 0,017. Поправка Бонферрони хорошо контролирует ошибку 1 типа, но является очень консервативной и приводит к повышению вероятности ошибки 2 типа (вероятности принятия решения об отсутствии различий там, где они на самом деле есть). Либеральные критерии, (например критерий Тьюки) в свою очередь, завышают вероятность ошибки 1 типа, то есть вероятность принятия решения о наличии различий там, где их нет.
Таким образом, при выборе статистического критерия для апостериорных сравнений необходимо принимать во внимание, как критерии контролируют ошибки 1 и 2 типов и как они работают при несоблюдении необходимых условий применения дисперсионного анализа.
Если данные не подчиняются нормальному распределению, то при анализе можно использовать два способа: применением различных арифметических преобразований до достижения нормальности распределения и дальше уже применять дисперсионный анализ, или использовать критерий Краскела-Уоллиса (Kruskal-Wallis H-test), иногда его также называют непараметрическим дисперсионным анализом. Как и в большинстве непараметрических методов, работающих с количественными данными, исходный набор данных преобразуется в ранги и обрабатывается уже он. При обнаружении статистически значимых различий между группами стоит дальше проводить апостериорные сравнения с использованием критерия Манна-Уитни.
Пример
В условиях крупной городской клинической больницы было решено провести исследование по оценке влияния возраста на длительность госпитализации после лапароскопической холецистектомии. 9 пациентов были разделены на 3 группы в зависимости от возраста
Длительность госпитализации
после лапароскопической холецистектомии в зависимости от возраста, дни
| Группа №1Младше 45 лет | Группа №245-55 лет | Группа №3Старше 55 лет |
| 3 | 5 | 7 |
| 1 | 3 | 6 |
| 2 | 4 | 5 |
| x̄=2 | x̄=4 | x̄=6 |
Сделайте выводы о влиянии возраста на длительности госпитализации после лапароскопической холецистектомии.
- Постановка нулевой гипотезы
H0 указывает на отсутствие различий между группами, иными словами все группы по возрасту относятся к одной генеральной совокупности и соответственно средние равны друг другу
µ1= µ2= µ3
Альтернативная гипотеза выдвигает предположение, что длительно госпитализации зависит от возраста и средние в этих группах на самом деле не равны
µ1≠ µ2≠ µ3
- Найдем общую сумму квадратов
Для этого нам нужно знать общую среднюю по всем выборкам, найдем ее:
x̄= (2+3+6)=4
SST =2 = (3-4)2+(1-4) 2+(2-4) 2+(5-4) 2+(4-4) 2+(3-4) 2+(7-4) 2+
+(6-4) 2+(5-4) 2=30
- Найдем сумму квадратов внутри групп последовательно вычитая из каждого значения в группе групповую среднюю:
SSWG = (3-2)2 + (1-2) 2 + (2-2) 2 + (5-4) 2 + (3-4) 2 + (4-4) 2 + (7-6) 2 + (6-6) 2 + (5-6)2 =2+2+2=6
- Найдем внутригрупповую сумму квадратов.
Для этого нам необходимо найти квадрат отклонения каждой из выборочных средних относительно общей вредней:
SSBG =3(2-4)2+3(4-4)2+3(6-4)2=24
- Найдем значение критерия Фишера, исходя из средних квадратов отклонений внутри групп и между ними и соответствующих степеней свободы:
νBG = m – 1 = 3-1 = 2
νWG = n – m = 9 – 3 = 6
F= 12, Fкрит. = 5,143 при α = 0,05
F > Fкрит
- Делаем вывод о наличии статистически значимых отличий между группами:
так как наше значение F больше критического значения при заданном количестве наблюдений и количестве групп, иными словами наша дисперсия между группами вносит больший вклад в любую сумму дисперсий, чем таковая внутри самих групп.
Возраст влияет на длительность госпитализации после холецистектомии.
[1] Sum of squares between groups
[2] Sum of squares within groups
[3]MSBG — Средний квадрат отклонения между группами и MSWG — Средний квадрат отклонения внутри групп