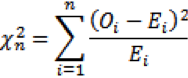Хи-квадрат (χ2) Пирсона: условия применения метода и интерпретация
Хи-квадрат Пирсона один из самых популярных статистических критериев для анализа качественных данных (номинальных, порядковых, ранговых), анализа частот. Однако, как и у каждого статистического критерия у хи-квадрата есть свои собственные правила применения метода, его интерпретации. Для того, чтобы Вы могли успешно овладеть этим ценнейшим статистическим инструментом сравнения статистических совокупностей по качественным данным предлагаем Вам ознакомиться с этой учебной статьей.
Правила использования хи-квадрата Пирсона
Условия применения хи-квадрата Пирсона
Как рассчитывать хи-квадрат Пирсона
Учет степеней свободы при применении хи-квадрата Пирсона
Пример корректной интерпретации хи-квадрата Пирсона
Видео-версия статьи
Как использовать хи-квадрат Пирсона?
Хи-квадрат используется прежде всего для анализа таблиц сопряженности (вид таблицы, которая учитывает совместное влияние фактора на исход, данные в таблице сопряженности должны быть представлены в виде частоты номинальных данных или интервалами, но не непрерывными количественными величинами). Стоит отметить, что при работе с сопряженными таблицами хи-квадрат часто является поддержкой для анализа влияния факторов риска с помощью расчета рисков (абсолютный и относительный риски) и отношение шансов.
Таблицы сопряженности могут принимать различные формы, простейшая таблица сопряженности выглядит следующим образом:
| Исход есть | Исхода нет | Всего | |
| Фактор риска есть | A | B | A+B |
| Фактора риска нет | C | D | C+D |
| Всего | A+C | B+D | A+B+C+D |
Как заполнить таблицу сопряженности? Обратимся к простому примеру:
Например, Вы хотите с помощью таблицы сопряженности и как следствия хи-квадрата Пирсона выяснить есть ли различия в частоте артериальной гипертонии в группах курящего и некурящего населения. Предполагается, что по остальным параметрам Ваши группы равномерны и превалирующим фактором риска развития артериальной гипертензии будет именно курение.
Для проведения исследования на основании ретроспективных данных (дизайн: случай-контроль) были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую группу вошли 80 некурящих такого же возраста, пола, и социального уровня (прочие систематически ошибки случайны).
В первой группе у 40 человек отмечалась артериальная гипертензия. Во второй — у 32 человек. Соответственно, референсное (нормальное) артериальное давление в группе «курильщиков» наблюдалось у 30 человек (70 — 40 = 30), а в группе «некурящих» нормальное АД наблюдалось у 48 (80 — 32 = 48).
Имея эти данные мы можем заполнить простейшую таблицу сопряженности:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
АД- артериальное давление
Как видно из таблицы: каждая строка соответствует группе пациентов, которая подвергается влиянию фактора, каждый столбец, в свою очередь, обозначает частоту исходов в группе (к примеру: произошло/ не произошло, как в нашем примере).
Таблицы сопряженности служат удобным средством визуализации комбинации частот «фактор- исход» и субстратом для расчета хи-квадрата Пирсона, который в нашем случае сможет дать статистически точный ответ о случайности или не случайности наших находок.
Условия применения статистического критерия хи-квадрата Пирсона
- Тип данных: параметры должны быть качественными цельночисленными частотами, измеренными в номинальной шкале (Например, тип диагноза)
бинарными (пол: мужской/женский, наличие или отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
- Желательно, чтобы общее количество наблюдений было более 20,
- Ожидаемая частота, соответствующая нулевой гипотезе должна быть более 5, если ожидаемое явление принимает значение менее 5, то необходимо использовать точный Критерий Фишера.
- Для четырехпольных таблиц (2х2): Если ожидаемое значение принимает значение менее 10 (а именно 5<x<10), необходим расчет поправки Йетса таблиц сопряженности
- Сравниваемые частоты должны быть примерно одного размера
- Сопоставляемые группы должны быть независимыми (то есть единицы наблюдения в них разные, в отличие от связанных групп, анализирующих изменения «до-после» у одних и тех единиц наблюдений до и после вмешательства. Для таких ситуаций существует отдельный тест МакНемара (McNemar)
Запрещается: использовать хи-квадрат для анализа непрерывных абсолютных данных, процентов и долей
Как рассчитать критерий хи-квадрат Пирсона?
Для оценки достоверности различий по методу хи-квадрата Пирсона (критерий соответствия, коэффициент согласия) анализируется различия между реальной существующими частотами в группах (Observed) и рассчитываемыми по формуле ожидаемыми «гипотетическими» частотами, которые соответствуют распределению хи-квадрат. При малом различии ожидаемых и наблюдаемых частот (хи-квадрат не достиг своего критического значения) мы принимаем нулевую гипотезу об отсутствии различий. Если же различия оказываются существенными (критическое значение хи-квадрата достигаются для заданного числа степеней свободы) мы отвергаем нулевую гипотезу и говорим о наличии статистически значимых различий.
Чем больше теоретические числа, рассчитанные на основе Но-гипотезы, будут отличаться от фактических, тем более «хи -квадрат» будет отличаться от 0, тем с большей вероятностью можно отклонить Но-гипотезу и говорить о статистической достоверности имеющихся различий в сравниваемых совокупностях.
Основная формула для расчета хи-квадрата Пирсона:
Зачем учитывать количество степеней свободы при расчете хи-квадрата?
Для того, чтобы не утомлять читателя пространными разъяснениями «о сумме квадратом нормально распределенных случайных величин» скажем лишь, что оценка критического значения хи-квадрата зависит от степени свободы изменения частот, что это значит на практике для пользователя хи-квадрата? То, что чем более многопольная таблица перед Вами, тем больше степеней свободы, чем она меньше, тем меньше. Формула расчета хи-квадрата следующая:
Degree of freedom (d.f.) = (c-1)(r-1)
Column (c) – количество столбцов частотами, r- количество строк с частотами.
Таким образом, количество степеней свободы для стандартной 2х2 таблицы сопряженности составит:
d.f. = (2-1)*(2-1)=1
и так далее.
Примеры расчета хи-квадрата Пирсона
Пример 1:
Необходимо определить наличие влияния предшествующей степени нарушения кровообращения на исход комиссуротомии (хирургическое разделение спаек при стенозе клапанного отверстия сердца). Пациенты поступали на комиссуротомию с различными исходными уровнями нарушения кровообращения. После комиссуротомии пациенты были выписаны с различными исходами операции.
Фактор: Степень нарушения кровообращения
Исход: Результативность операции
Таблица: наблюдаемые (Observed) частоты распределения влияния степени нарушения кровообращения на результаты операции комиссуротомии
| Степень нарушения кровообращения | Всего больных | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 30 | 20 | 8 | 2 |
| III | 80 | 43 | 20 | 17 |
| IV | 60 | 10 | 40 | 10 |
| Всего | 170 | 73 | 68 | 29 |
| H0-гипотеза | 100% | 43% | 40% | 17% |
Первый этап
Расчет ожидаемых (Expected) величин (на основании групповых частот)
Второй этап
Сопоставление наблюдаемых и ожидаемых частот с нахождением их разницы (O-E)
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | +7 | -4 | -3 |
| III | +9 | -12 | +3 |
| IV | -16 | +16 | 0 |
| Всего | 0 | 0 | 0 |
Третий этап
Рассчитываем сумму отношений квадрата разности значений и делим ожидаемые данные (хи-квадрат) (O-E)2/E
| Степень нарушения кровообращения | Выписан с хорошим результатом операции | Выписан с удовлетворительным результатом операции | Выписан с ухудшением |
| II | 49/13=3,77 | 16/12=1,33 | 9/5=1,80 |
| III | 81/34=2,38 | 144/32=4,50 | 9/14=0,64 |
| IV | 256/26=9,85 | 256/24=10,66 | 0/10*=0,10 |
| Всего | 16 | 16,49 | 2,54 |
как видно из данной таблицы одно из ожидаемых значений равно 0, в данном случае будет подставлена 1, корректнее применить точный критерий Фишера (см. Условия применения хи-квадрата Пирсона)
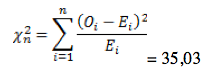
Четвертый этап
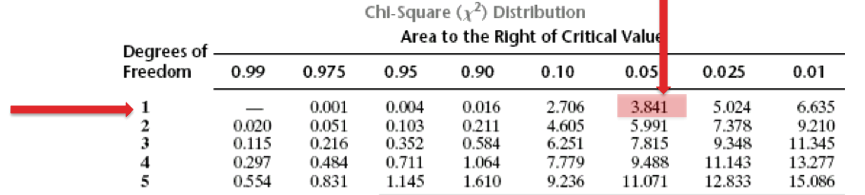
Необходимо соотнести полученное значение хи-квадрата с критическим значением хи-квадрата.Возникает вопрос, откуда брать критическое значение? Критическое значение хи-квадрата, как и для большинства, статистических критериев зависит от степени свободы и уровня достоверности (alpha), который Вы выбираете.В нашем случае, наше количество степеней свободы равно (3-1)*(3-1)=4, уровень значимости, который мы хотим соблюсти равен 0,05Обратимся к таблице критических значение хи-квадрата: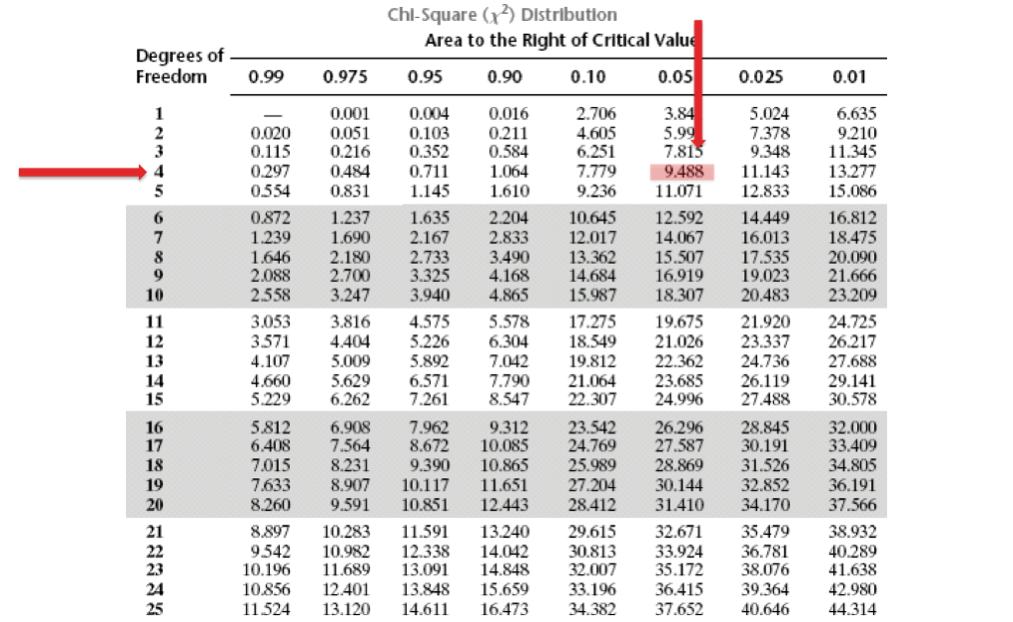
- Xи-квадрат (для d.f.=4 p=0.05) = 9.488
- Xи-квадрат (для d.f.=4 p=0.01) = 13.27735,03 > 13,277;
- p<0,01
Пример корректной интерпретации: Предшествующая степень нарушения кровообращения влияет на исход комиссуротомии (однако! Мы не можем говорить о направленности связи, то есть: улучшает-ухудшает сказать не можем), оптимально указать степень свободы, точное значение хи-квадрата, если есть возможность рассчитать точное значение достоверности, то так же стоит указать и его или остановиться на критическом значении достоверности (p<0,05 или p<0,01 и так далее).В нашем случае:d.f.=4, x2=35,03, p< 0.01
Пример 2: Вернемся к нашему примеру с влиянием курения на развитие артериальной гипертензии:Исходная четырехпольная таблица:
| Повышенное АД | АД в пределах норма | Всего | |
| «Курильщики» | 40 | 30 | 70 |
| «Не курят» | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
Для четырехпольных таблиц существует упрощенная формула расчета значения хи-квадрата:
| Исход + | Исход 0 | Всего | |
| Фактор + | a | b | a+b |
| Фактор 0 | c | d | c+d |
| Всего | a+c | b+d | N |
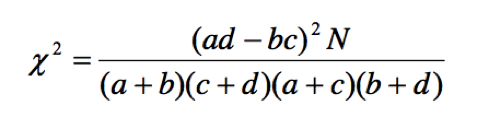
- x2= (40х48 – 32х30)х150 / (70)(80)(72)(78) = (1920 – 960)2х150/31449600 = 138240000/31449600 = 4,395
- Сравним полученное значение хи-квадрата с критическим значением (для степени свободы 1, и уровнем значимости 3,841)
Правильная интерпретация: Курение оказывает влияние на формирование повышенного артериального давления df=1, x2= 4,395, p<0,05
Заключение по хи-квадрату Пирсона
хи-квадрат Пирсона является удобным статистическим методом для анализа изменения частот, оформленными в таблицы сопряженности для несвязанных групп. Как и все статистически инструменты хи-квадрат Пирсона имеет свои правила, преимущества и ограничения применения. Будьте внимательны и хи-квадрат Пирсона Вас не разочарует.