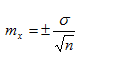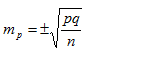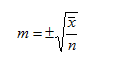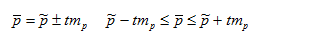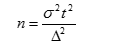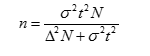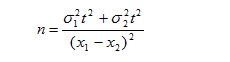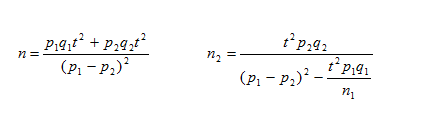Выборочный метод — точная характеристика изучаемых совокупностей
The W10295370 has been updated by Whirlpool and released as the new and improved EveryDrop EDR1RXD1. Indulge yourself with better tasting water and ice with the Whirlpool W10295370 compatible refrigerator water and ice filter. Also known as the EDR1RXD1 and Filter1. Before water reaches your home it goes through a long treatment process that doesn’t always get all the bad stuff out, and usually leaves behind unpleasant tastes and odors. The aftertaste in your mouth is linked to chlorine used in public water supplies. While efficient as a disinfectant, the taste can make many people turn to sugary juices and bottled water as an alternative.
Replaced model w10295370a
the Whirlpool w10295370a . compatible helps reduce those tastes and odors making the water you drink more refreshing. That same filter media is also NSF Standard 42 and 53 Certified to capture industrial chemicals, lead, and cysts among several other pollutants that are sometimes found in water inside homes. Beneficial fluoride is not removed to keep your smile bright as you enjoy the benefits a new refrigerator ice and water filter can bring.
Выборочный метод — точная характеристика изучаемых совокупностей
Задача, которую решает использование выборочного метода, заключается в возможности с минимальными данными выборки обеспечить получение максимально точных данных. Без применения знаний выборочного наблюдения и выборочной совокупности невозможно оценить масштабные клинические исследования, наблюдения, спрогнозировать различные явления и обрабатывать первичные данные.
Выборочное наблюдение — вид несплошного наблюдения, при котором отбор подлежащих обследованию единиц наблюдения из генеральной совокупности(population) осуществляется случайно, отобранная часть (выборка) (sample)подвергается обследованию, после чего результаты распространяются на всю исходную совокупность. Выборка должна отвечать критериям качественной и количественной репрезентативности.
Рис. 1 Количественная и качественная репрезентативность выборки (Е.Н. – единица наблюдения).
Положительные стороны выборочного метода:
- может быть единственно доступным способом сбора данных, если единицы
наблюдения во время исследования подвергаются порче или уничтожению; - экономичность;
- сжатые сроки исследования, что ускоряет получение результата;
— большая точность получения результата за счет уменьшения случайных
ошибок при сборе материала;
— возможность задать надежность и точность исследования.
Отрицательные стороны выборочного метода:
- неизбежна ошибка в исследовании, связанная с тем, что не все единицы
наблюдения подвергаются отбору; - может быть нежелательным, если по официальным предписаниям необхо-
димо регистрировать каждую единицу наблюдения; - для редких событий малые выборки могут не накопить достаточного числа
случаев; - при социологических исследованиях может вызвать чувство дискриминации
у населения.
Эпидемиологические аспекты выборочного исследования будут подробно рассмотрены в соответствующем разделе (часть 2). Здесь мы остановимся на статистических аспектах данной проблемы, хотя эти два подхода неразрывно связаны между собой, составляя единую оболочку для научного исследования.
Основное требование, предъявляемое к формированию выборки – случайность отбора единиц наблюдения из генеральной совокупности, при котором каждой единице наблюдения обеспечивается равная вероятность попадания в выборку (рандомизированный отбор) (randomization).
Виды выборок
- В зависимости от способа отбора единиц наблюдения (от способа организации совокупности):
- случайная: отбор единиц наблюдения производится непосредственно из генеральной совокупности. Случайность отбора достигается путем применения жеребьевки или использования таблицы случайных чисел. Различают бесповторную выборку и повторную (после регистрации единицы вновь возвращаются в генеральную совокупность)
- механическая: генеральная совокупность разбивается на равные части, из которых затем в заранее обусловленном порядке отбирают единицы наблюдения под определенным номером (например, каждую пятую), так, чтобы обеспечить необходимое число наблюдений.
- типологическая (типическая): генеральная совокупность разбивается на качественно однородные по изучаемому признаку группы, а затем из этих групп производят случайный отбор необходимого числа единиц наблюдения; объем выборки в каждой типической группе устанавливается пропорционально ее удельному весу в генеральной совокупности (пропорциональный отбор), а иногда и с учетом вариации в ней изучаемого признака (оптимальный отбор)
- серийная (гнездовая): отбору подлежат не отдельные единицы наблюдения, а целые их группы (серии или гнезда), в составе которых единицы наблюдения связаны определенным образом: территориально (районы, селения и др.) или организационно (студенческие группы, больницы, предприятия и др.) и которые отбираются из генеральной совокупности по принципу случайного или механического отбора. Внутри серии производится сплошной отбор единиц наблюдения.
- комбинированная
- По этапам отбора:
- одноступенчатая
- многоступенчатая
- В зависимости от числа программ отбора:
- однопрограммная (однорядная)
- многопрограммная (многорядная)
Модификации видов выборок:
- метод направленного отбора
- метод парных выборок
- когортный метод
- метод моментного среза
Теоретическая основа выборочного метода
Взаимосвязь статистических показателей выборочной и генеральной совокупностей определяется законом больших чисел, выражаясь в центрально предельной теореме П. Л. Чебышева: чем больше число некоторых случайных величин, тем их средняя арифметическая ближе к средней арифметической генеральной совокупности, т.e. тем меньше разница между показателями выборочной и генеральной совокупностей. По мере увеличения числа наблюдений вероятность осуществления приближения показателя выборки к показателю генеральной совокупности становится все больше, стремясь к единице, если число наблюдений стремится к бесконечности. Для того, чтобы могла проявиться эта закономерность, выборка должна быть репрезентативна (представительна) по отношению к генеральной совокупности.
Репрезентативность — это способность выборочной совокупности как количественно, так и качественно отражать свойства генеральной совокупности. Количественная репрезентативность достигается достаточностью числа наблюдений, качественная — соответствием признаков единиц наблюдения в выборочной и генеральной совокупностях.
Любое значение параметра, вычисленное на основе ограниченного числа наблюдений, непременно содержит элемент случайности. Такое приближенное, случайное значение называется оценкой параметра. Оценка параметра должна быть доброкачественной, что определяется тремя факторами, которые дают наименьшие ошибки расхождения показателей выборочной и генеральной совокупностей:
- состоятельность оценки, т.е. при увеличении числа наблюдений оценка параметра приближается к его значению в генеральной совокупности;
- несмещенность оценки, т.е. при оценке отсутствуют систематические ошибки в сторону завышения или занижения параметра генеральной совокупности;
- эффективность оценки, т.е. оценка должна обладать минимальной вариабельностью.
Как правило, проводят точечную и интервальную оценку параметра.
Точечная оценка параметра
Точечная оценка параметра выражается в ошибке репрезентативности (standard error, стандартной ошибке), которая показывает на сколько отличаются обобщающие коэффициенты (показатели), полученные при выборочном исследовании, от тех коэффициентов, которые могли бы быть получены при сплошном исследовании.
Вычисление ошибки репрезентативности (m):
при показателях (коэффициентах), близких к 0 или к 100%: 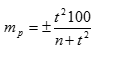
- При распределении Пуассона:
s- стандартное отклонение (sample variance)
n — число наблюдений в выборке (sample size)
р — частота появления признака в совокупности (significance level)
q — показатель, альтернативный
t — доверительный коэффициент
x — средняя величина (sample mean)
Способы, уменьшающие ошибку репрезентативности:
- увеличение числа наблюдений
- уменьшение вариабельности признака
Интервальная оценка параметра
Знание величины ошибки репрезентативности недостаточно, чтобы быть уверенным в результатах выборочного исследования, т.к. конкретная ошибка одного выборочного наблюдения может быть больше (меньше) средней ошибки выборки. Поэтому на практике определяют так же пределы возможных ошибок выборки или предельную ошибку выборки (D). Т.к. предельная ошибка может быть как в сторону увеличения, так и в сторону уменьшения, то говорят о доверительном интервале (ДИ) или доверительных границах (confidence interval, CI), в пределах которых будет находиться показатель генеральной совокупности на основании данных выборочного исследования
Выход результата за пределы доверительных границ в следствие случайных колебаний имеет незначительную вероятность. Пределы возможных отклонений, выраженные в долях t, оценивают по формуле:
Существует таблица соответствия интеграла вероятности и значения “t” (таблица Стьюдента). При числе наблюдений больше 30 можно пользоваться следующей закономерностью: вероятности безошибочного прогноза р = 0,68 приблизительно соответствует t @ 1; при p = 0,95 t @ 2, при р = 0,99 t @ 3. Это согласуется с «правилом трех сигм», когда в границах одного среднеквадратичного отклонения лежат 68% значений, двух – 95%, трех – 99%. Буква t в данном случае обозначает использование распределения Стьюдента.
При малом числе наблюдений (не более 30) вероятности нахождения выборочных значений в пределах значений t, которые характерны для больших выборок, значительно снижаются, т.е. для достижения тех же вероятностей нужно взять значительно большие интервалы x ± tm. В этих случая оперируют значениями t, приведенными в таблице Стьюдента.
Для большинства медицинских исследований допускают р = 0,95 или 95%. В этом случае вероятность выхода результата выборочного исследования за границы доверительного интервала, т.е. вероятность ошибки составляет 0,05 или 5%. Поэтому говорят, что результат исследования получен с уровнем значимости 0,05 (р=0,05). При необходимости более строгой оценки р=0,99 (99%), вероятность ошибки составит 0,01 (1%) и следовательно уровень значимости будет р=0,01.
Часто на практике необходимо оценить надежность и точность исследования, т.е. нужно знать, к каким ошибкам может привести замена параметра (результата в генеральной совокупности) его точечной оценкой (результатом в выборке с учетом ошибки репрезентативности) и с какой уверенностью можно ожидать, что эти ошибки не выйдут за известные пределы.
Точность оценки определяется доверительным интервалом (границами), надежность оценки определяется доверительной вероятностью, с которой оценка воспроизводится в пределах доверительных границ. Чем выше точность исследования, тем меньше его надежность. В результате при больших доверительных границах, уровень вероятности (или уровень значимости) может не достигать значений, принятых для медицинских исследований
Определение доверительных границ (доверительного интервала)
-для количественных признаков
— для номинальных и порядковых признаков
- По специальным таблицам с заданной предельной ошибкой (таблица Боярского).
- По формулам:
а) для количественных признаков:
- при неизвестной численности генеральной совокупности:
- при известной численности генеральной совокупности:
б) для номинальных и порядковых признаков:
- при неизвестной численности генеральной совокупности:
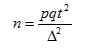
- при известной численности генеральной совокупности:
в) при выборке по методу контрольных групп или парных групп:
если число наблюдений в группах одинаково:
— для количественных признаков:
если число наблюдений в группах неодинаково:
— для количественных признаков: 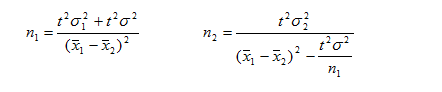
-для номинальных признаков:
Условные обозначения:
s – стандартное отклонение;
t — доверительный коэффициент,
n — число наблюдений в выборке;
D — предельная ошибка выборки;
р — частота появления признака в совокупности;
q — показатель, альтернативный p;
N – число наблюдений в генеральной совокупности.
Расчет объема выборки производят на начальных этапах исследования, когда неизвестны параметры распределения и предельная ошибка. Источниками для определения s и D служат:
— результаты пилотажного исследования;
— данные литературы (аналогичные исследования);
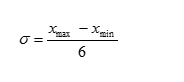
Как крайний вариант определения этих параметров для альтернативного распределения можно взять максимально возможное значение s2= р х q =0.5 x 0.5 = 0,.25, что существенно увеличивает необходимый объем наблюдений. Для количественных признаков приблизительное значение s можно определить как,
что также увеличивает необходимый объем выборки.
3. Объем выборки зависит от чувствительности критерия. С увеличением объема выборки чувствительность критерия увеличивается. Расчет чувствительности – важный этап планирования исследования.
Таким образом, итогом изучения материалов статьи для специалистов станут понятными главные определения и понятия, методы формирования репрезентативной выборки, определение точечной и интервальной оценки параметров. Кром того, предоставленные данные помогут сформировать репрезентативную по количеству и качеству выборку, вычислять ошибку репрезентативности (стандартную ошибку) для средних и долевых (частотных) величин в больших и малых выборках, вычислять ошибку репрезентативности (стандартную ошибку) для средних и долевых (частотных) величин в больших и малых выборках.
Благодарим за внимание к нашим материалам, оставайтесь с нами!